Колебания системы хищник-жертва (модель Лотки-Вольтера). Колебания системы хищник-жертва (модель Лотки-Вольтера) Модель системы хищник жертва с логистической поправкой

Часто представители одного вида (популяции) питаются представителями другого вида.

Модель Лотки – Вольтерры – модель взаимного существования двух популяций типа «хищник – жертва».

Впервые модель «хищник – жертва» была получена А. Лоткой в 1925 году, который использовал ее для описания динамики взаимодействующих биологических популяций. В 1926 году независимо от Лотки аналогичные (к тому же более сложные) модели были разработаны итальянским математиком В. Вольтерра, глубокие исследования которого в области экологических проблем заложили фундамент математической теории биологических сообществ или т. н. математической экологии.

В математической форме предложенная система уравнений имеет вид:

где x – количество жертв, y – количество хищников, t – время, α, β, γ, δ – коэффициенты, которые отражают взаимодействия между популяциями.

Постановка задачи

Рассмотрим закрытое пространство, в котором существуют две популяции – травоядные («жертвы») и хищники. Считается, что животных не ввозят и не вывозят и что еды для травоядных животных достаточно. Тогда уравнение изменения числа жертв (только жертв) примет вид:

где $α$ – коэффициент рождаемости жертв,

$x$– размер популяции жертв,

$\frac{dx}{dt}$ – скорость прироста популяции жертв.

Когда хищники не охотятся, они могут вымирать, значит, уравнение для количества хищников (только хищников) примет вид:

Где $γ$ – коэффициент убыли хищников,

$y$ – размер популяции хищников,

$\frac{dy}{dt}$ – скорость прироста популяции хищников.

При встрече хищников и жертв (частота встреч прямо пропорциональна произведению) хищники уничтожают жертв с коэффициентом, сытые хищники могут воспроизводить потомство с коэффициентом. Таким образом, система уравнений модели примет вид:

Решение задачи

Построим математическую модель совместного существования двух биологических популяций типа «хищник – жертва».

Пусть две биологические популяции совместно обитают в изолированной среде. Среда является стационарной и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов – жертвы. Другой вид – хищник – также обитает в стационарных условиях, но питается только жертвами. В роли хищников могут выступать коты, волки, щуки, лисы, а в роли жертв – куры, зайцы, караси, мыши соответственно.

Для определенности рассмотрим в роли хищников – котов, а в роли жертв – кур.

Итак, куры и коты живут в некотором изолированном пространстве – хозяйственном дворе. Среда предоставляет курам питание в неограниченном количестве, а коты питаются только курами. Обозначим через

$х$ – количество кур,

$у$ – количество котов.

Со временем количество кур и котов меняется, но будем считать $х$ и $у$ непрерывными функциями от времени t. Назовем пару чисел $х, у)$ состоянием модели.

Найдем каким образом изменяется состояние модели $(х, у).$

Рассмотрим $\frac{dx}{dt}$ – скорость изменения количества кур.

Если котов нет, то количество кур возрастает и тем быстрее, чем больше кур. Будем считать зависимость линейной:

$\frac{dx}{dt} a_1 x$,

$a_1$ – коэффициент, который зависит только от условий жизни кур, их естественной смертности и рождаемости.

$\frac{dy}{dt}$ – скорость изменения количества котов (если нет кур), зависит от количества котов y.

Если кур нет, то количество котов уменьшается (у них нет пищи) и они вымирают. Будем считать зависимость линейной:

$\frac{dy}{dt} - a_2 y$.

В экосистеме скорость изменения количества каждого вида также будем считать пропорциональным его количеству, но только с коэффициентом, зависящим от количества особей другого вида. Так, для кур этот коэффициент уменьшается с увеличением количества котов, а для котов возрастает с увеличением количества кур. Будем считать зависимость также линейной. Тогда получим систему дифференциальных уравнений:

Данная система уравнений называется моделью Вольтерра-Лотки.

a1, a2, b1, b2 – числовые коэффициенты, которые называют параметрами модели.

Как видно, характер изменения состояния модели (x, y) определяется значениями параметров. Изменяя данные параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы.

С помощью программы MATLAB система уравнений Лотки-Вольтерра решается следующим образом:

На рис. 1 представлено решение системы. В зависимости от начальных условий решения разные, чему отвечают разные цвета траекторий.

На рис. 2 представлены те же решения, но с учетом оси времени t (т.е. наблюдается зависимость от времени).

Простейшая модель взаимоотношений популяций хищника и жертвы, основанная на логистическом уравнении роста, названа (как и модель межвидовой конкуренции) по имени ее создателей - Лотки и Вольтерры. Эта модель крайне упрощает исследуемую ситуацию, но все же полезна в качестве отправной точки в анализе системы хищник-жертва.

Предположим, что (1) популяция жертвы существует в идеальной (независимой от плотности) среде, где ее рост может ограничивать только наличие хищника, (2) столь же идеальна среда, в которой существует хищник, рост популяции которого ограничивает лишь обилие жертв, (3) обе популяции размножаются непрерывно согласно экспоненциальному уравнению роста, (4) скорость поедания жертв хищниками пропорциональ­на частоте встреч между ними, которая, в свою очередь, является функцией плотности популяций. Эти допущения и лежат в основе модели Лотки - Вольтерры.

Пусть в отсутствие хищников популяция жертвы растет экспоненциаль­но:

где N -численность, а r, - удельная мгновенная скорость роста популя­ции жертвы. Если же хищники присутствуют, то они уничтожают особей жертвы со скоростью, которая определяется, во-первых, частотой встреч хищников и жертв, возрастающей по мере увеличения их численностей, и, во-вторых, эффективностью, с которой хищник обнаруживает и ловит свою жертву при встрече. Число жертв, встреченных и съеденных одним хищником N с, пропорционально эффективности охоты, которую мы выразим через коэффициент С 1; численности (плотности) жертвы N и времени, затраченному на поиски Т:

N C =C 1 NT (1)

Из этого выражения легко определить удельную скорость потребления жертв хищником (т.е. число жертв, поедаемых одной особью хищника в единицу времени), которую часто называют также функциональным ответом хищника на плотность популяции жертвы:

В рассматриваемой модели С 1 является константой. Это означает, что число жертв, изъятых хищниками из популяции, линейно возрастает с увеличением ее плотности (так называемый функциональный ответ типа 1). Ясно, что общая скорость поедания жертв всеми особями хищника составит:

где Р - численность популяции хищника. Теперь мы можем записать уравнение роста популяции жертвы следующим образом:

При отсутствии жертвы особи хищника голодают и гибнут. Предполо­жим также, что в этом случае численность популяции хищника будет уменьшаться экспоненциально согласно уравнению:

где r 2 - удельная мгновенная смертность в популяции хищника.

Если жертвы присутствуют, то те особи хищника, которые смогут их найти и съесть, будут размножаться. Рождаемость в популяции хищника в данной модели зависит только от двух обстоятельств: скорости потребления жертв хищником и эффективности, с которой поглощенная пища перерабатывается хищником в его потомство. Если мы выразим эту эффективность через коэффициент s, то рождаемость составит:

Поскольку С 1 и s - константы, их произведение - это также константа, которую мы обозначим как С 2 . Тогда скорость роста популяции хищника будет определяться балансом рождаемости и смертности в соответствии с уравнением:

Уравнения 4 и 6 вместе образуют модель Лотки-Вольтерры.

Свойства этой модели мы можем исследовать точно так же, как и в случае конкуренции, т.е. построив фазовую диаграмму, на которой численность жертвы отложена по оси ординат, а хищника - по оси абсцисс, и проведя на ней изоклины-линии, соответствующие постоян­ной численности популяций. С помощью таких изоклин определяют поведение взаимодействующих популяций хищника и жертвы.

Для популяции жертвы: при откуда

Таким образом, поскольку r, и С 1 , - константы, изоклиной для жертвы будет линия, на которой численность хищника (Р) является постоянной, т.е. параллельная оси абсцисс и пересекающая ось ординат в точке Р =r 1 / С 1 . Выше этой линии численность жертвы будет уменьшаться, а ниже- возрастать.

Для популяции хищника:

при откуда

Поскольку r 2 и С 2 - константы, изоклиной для хищника будет линия, на которой численность жертвы (N) является постоянной, т.е. перпендикуляр­ная оси ординат и пересекающая ось абсцисс в точке N = r 2 /С 2 . Слева от нее численность хищника будет уменьшаться, а справа - возрастать.

Если мы рассмотрим эти две изоклины вместе, то легко заметим, что взаимодействие популяций хищника и жертвы имеет циклический характер, поскольку их численности претерпевают неограниченные сопряженные колебания. Когда велико число жертв, численность хищников растет, что приводит к увеличению пресса хищничества на популяцию жертвы и тем самым к снижению ее численности. Это снижение, в свою очередь, ведет к нехватке пищи у хищников и падению их численности, которое вызывает ослабление пресса хищничества и увеличению численности жертвы, что снова приводит к росту популяции жертвы и т.д.

Для данной модели характерна так называемая "нейтральная стабиль­ность", которая означает, что популяции неограниченно долго совершают один и тот же цикл колебаний до тех пор, пока какое-либо внешнее воздействие не изменит их численность, после чего популяции совершают новый цикл колебаний с иными параметрами. Для того, чтобы циклы стали стабильными, популяции должны после внешнего воздействия стремиться вернуться к первоначальному циклу. Такие циклы, в отличие от нейтрально стабильных колебаний в модели Лотки-Вольтерры, принято называть устойчивыми предельными циклами.

Модель Лотки-Вольтерры, тем не менее, полезна тем, что позволяет продемонстрировать основную тенденцию в отношениях хищник-жертва возникновение циклических сопряженных колебаний численности их популяций.

Изв. вузов «ПНД», т. 19, № 2, 2011

ФЕНОМЕН МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЛОТКИ-ВОЛЬТЕРРЫ И СХОДНЫХ С НЕЙ*

Д.И. Трубецков

Математическая модель Лотки-Вольтерры (часто её называют моделью «хищник-жертва») применима для описания различных процессов в биологии, экологии, медицине, в социальных исследованиях, в истории, в радиофизике и других науках.

В настоящем обзоре, который во многом носит методологический характер, рассмотрены варианты этой модели и сходных с ней применительно к анализу ряда природных и социальных явлений.

Обсуждаются следующие модели: модели взаимодействия загрязнения с окружающей средой; модель классовой борьбы; модель бесклассового общества эпохи охотников-собирателей; модель военных действий; вирусная модель инфекционного заболевания; модель распространения эпидемий, включая модель заражения вирусом компьютеров; модель взаимодействия когнитивных и/или эмоциональных мод мозга.

Ключевые слова: Математическая модель Лотки-Вольтерры, система «хищник-жертва», анализ природных и социальных явлений.

«...При разрешении юридических казусов, как и при постановке врачом диагноза или во время опытов, проводимых химиком, решающую* роль играет распознавание типовых моделей».

Бернхард Шлинк. Возвращение**

Введение на основе экологических примеров

По своей сути модель Лотки-Вольтерры есть математическое описание дарвинского принципа борьбы за существование, который Чарльз Дарвин в своей автобиографии излагает следующим образом. «Изучив множество обстоятельств, я пришел к выводу о существовании борьбы за существование. Однажды пришло мне в голову, что при подобных обстоятельствах благоприятные виды продолжили бы развиваться

"Санкт-Петербург: Издательская группа «Азбука-классика», 2010, с. 67

Путь, которым шел Дарвин, хорошо описан в книге . Любопытно, что Дарвин окончательно уверился в своих выводах после прочтения книги «Опыт о законе народонаселения» Томаса Роберта Мальтуса . Это эссе сыграло важную роль в социальной и политической жизни Британии в 90-е годы XVIII века, поскольку его воспринимали как разумное осмысление естественных законов общества. В 30-е годы XIX века мальтузианские доктрины подавляли проведение правительственной политики. Напомним доводы Мальтуса, которые удивительно просты. Поскольку, по словам Мальтуса, у человечества есть естественная склонность к увеличению рода, производство пищи не могло оставаться на прежнем уровне.

«Хотя приблизительный баланс существует, как утверждал автор: некоторое количество людей погибает в результате природных факторов (голода или болезней) или человеческих действий (войны, сексуальные воздержания или греховные поступки, например, детоубийство), Это необходимо ради общего баланса существования,

Мальтус пошел дальше, утверждая: ...данная участь (гибель) - удел самого слабого, самого бедного и самого Больного члена общества, Избежать уготованной судьбы не представляется возможным, на то есть воля Бога, Напрашивался один простой вывод, но автор предостерегал о нем: если дать нищим милостыню, то человеческий род будет увеличиваться, появится и нехватка пищи»,

Викторианское время, казалось бы, подтвердило правоту Мальтуса. Возникли мятежи, связанные с недостатком еды, дискуссии о «Законе о бедных» и общественная реакция на «Хлебные законы». В 1834 году викторианские правящие круги в ответ на поправки к «Закону о бедных» как альтернативу церковным благотворительным обществам организовали работные дома, где люди работали за хлеб и воду.

Дарвин жил в этом мире, был его представителем и вращался в одинаковых с Мальтусом кругах. Он распространяет идеи Мальтуса на все живое: в природе идет борьба за жизнь, борьба за существование, в которой худший и слабейший организм погибает первым, а побеждают более развитые формы, более здоровые и приспособленные. Именно эти особи дают потомство. Организмы быстрее адаптируются к условиям окружающей среды, если подобные случаи борьбы повторяются через некоторые промежутки времени.

Начнем дальнейшее изложение (в качестве напоминания) с моделей взаимодействующих популяций - первых математических моделей Лотки и Вольтерры . Будем следовать в изложении главе 5 книги , поскольку это удобно для дальнейшего описания моделей взаимодействия загрязнения с окружающей средой.

Авторы указывают в первую очередь на работу Вольтерры , замечая, что аналогичная модель «была предложена Лоткой несколько ранее (Воль-терра значительно более полно провел анализ этой системы, Лотка каждый раз старался подчеркнуть свой приоритет в записи этой модели)»,

Модель Лотки-Вольтерры описывает взаимодействие двух видов - популяции хищников и популяции жертв.

Пусть N(t) - численность жертв, P(t) - численность хищников в момент времени t. Тогда модель Лотки-Вольтерры имеет вид:

AN - bNP, - = -dP + cNP, (1)

a, b, c, d - положительные постоянные.

Напомним, что система уравнений (1) основана на следующих допущениях:

При отсутствии хищников жертвы размножаются неограниченно согласно уравнению dN/dt = aN, которое называют иногда уравнением Мальтуса;

Хищники при отсутствии жертв вымирают согласно уравнению dP/dt = -dP;

Слагаемые, пропорциональные произведению NP, рассматриваются как превращение энергии одного источника в энергию другого (эффект влияния популяции хищников на популяцию жертв, то есть результат их встречи, состоит в уменьшении скорости прироста dN/dt численности жертв на величину NP, пропорциональную численности хищников).

Если ввести новые переменные

() N(t)d () P(t)b

п(х) = -v(x) = -^,

то система уравнений (1) примет вид

N - nv, - = YV(n - 1), dx dx

Система уравнений (2) имеет две неподвижные точки: (0, 0) - седло и (1,1),

для которой собственные значения матрицы Якоби A

- ^1,2 = ±iVУ,

i = л/- 1, то есть положение равновесия (1,1) негиперболическое и сделать вывод о его устойчивости на основе линейного анализа нельзя.

Фазовые траектории системы уравнений (2), как известно, являются интегральными кривыми уравнения

dv (п - 1)v dn Y (1 - v)n’

решение которого

yn + v - ln nYv = H.

Можно показать (см., например, ), что вблизи (1, 1) линии уровня функции H представляют собой замкнутые кривые, соответствующие периодическим решениям системы уравнений (2) (рис. 1). Постоянная H в выражении (3) определяется начальными условиями, например, n(0) = n0 и v(0) = vo.

Математическая модель, описываемая системой уравнений (2), структурно

неустойчива, то есть малое изменение правых частей в ней может приводить к качественному изменению поведения решения. В этом её основной недостаток. Более того, именно поэтому трудно говорить о совпадении теории с экспериментом.

Одна из причин структурной неустойчивости модели в том, что она является консервативной, то есть имеет первый интеграл. Как подчеркивает автор книги , несмотря на указанный основной недостаток модели, система уравнений (1) позволяет сделать нетривиальные выводы, подтвержденные многочисленными наблюдениями. В частности, в сформулирован принцип Вольтерры: если в системе «хищник-жертва», описываемой моделью (1), оба вида истребляются равномерно и пропорционально числу их индивидуумов, то среднее число жертв возрастает, а среднее число хищников убывает.

В книге приведены два примера существования этого эффекта в природе. Один - общественный факт, который привел Вольтерру к его теории борьбы за существование : во время первой мировой войны лов рыбы в Адриатическом море был сильно сокращен, что, к удивлению биологов, привело к увеличению хищников и уменьшению числа жертв. Второй пример менее известен. Согласно , принцип Вольтерры показывает двойственный характер применения средств от насекомых (инсектицидов) для сохранения урожая на полях. Почти все такие химические вещества действуют не только на вредителей, но и на их естественных врагов, что зачастую приводит к увеличению числа вредителей и уменьшению, например, птиц, питающихся этими вредителями. Таким образом, согласно принципу Вольтерры, в экосистеме «хищник-жертва» популяция жертв более чувствительна к процессу пропорционального уменьшения особей в популяции.

В терминологии В.И. Арнольда, модель, описываемая системой уравнений (1), называется «жесткой» . Кстати, раздел книги В.И. Арнольда «Жесткие» и «мягкие» математические модели (М.: МЦНО, 2000) называется «Жесткие модели как путь к ошибочным предсказаниям». При малом изменении модели она становится мягкой, когда к правым частям (1) добавляются малые слагаемые, учитывающие, например, конкуренцию жертв за пищу или хищников за жертв (конкретные виды уравнений приведем ниже). Тогда в общем виде уравнения (1) можно переписать так:

В зависимости от малых поправок ef (P, N) и eg(P, N) возможны, например, сценарии, показанные на рис. 2.

В смысле интерпретации интересен рис. 2, б. По Арнольду, если P - бандиты, а N - трудящиеся, эволюция системы приводит то к резкому увеличению числа бандитов, то к их почти полному вымиранию, поскольку они настолько ограбили трудящихся, что взять уже нечего. Система в конечном счете попадает в область столь больших или столь малых значений P и N, что модель становится неприменимой, поскольку изменяются законы эволюции.

Приведем еще несколько усложненных моделей «хищник-жертва».

Система «хищник-жертва» с учетом внутривидовой конкуренции.

aN - bPN + ef (P, N)

dP + cPN + eg(P,N), e < 1.

Рис. 2. а - состояние равновесия устойчиво: при любых начальных условиях через большое время устанавливается оно же; б - состояние равновесия B внеустойчиво: система идет «вразнос»; в - в системе с неустойчивым стационарным состоянием А устанавливается с течением времени периодический режим С (в отличие от системы (1) (см. рис. 1) имеют место колебания определенной амплитуды, не зависящей от малости отклонения)

где K\,2 - потенциальные емкости экологических систем, которые определяются доступным количеством ресурсов и соответствуют предельным значениям численности популяций. В безразмерных переменных данная система уравнений примет вид

где N(t) = (a/c)u(x), P(t) = av(x)/b, т Модель конкуренции

at, у = d/a, a = a/(cK\), в = d/(aK2).

it1=1-Ш-eNN ж=1-f)-hNN (5)

Здесь n, r2, e, h - положительные постоянные.

Анализ системы уравнений (5) показывает: если n популяций линейно зависят от m ресурсов, причем m < n, то по крайней мере одна из популяций вымирает.

Модель мутуализма (симбиоза)

ui(ri + aiiui + ai2u2),

u2 (Г2 + a2iui + a22u2).

Для описания мутуализма достаточно потребовать, чтобы

ai2 > 0, a2i > 0.

Детальный анализ приведенных моделей можно найти, например, в книгах и .

В заключение раздела, следуя в изложении , рассмотрим обобщенную модель Лотки-Вольтерры, описываемую системой уравнений

A(u) - B(u,v), - = -D(v) + C (u,v), (7)

где u и v - численности жертв и хищников, соответственно, A(u) - функция размножения жертв при отсутствии хищников; D(v) - функция вымирания хищников при отсутствии жертв; функция B(u, v) описывает выедание хищниками жертв; C(u, v) -эффективность потребления жертв хищниками. Перечислим возможные дополнительные факторы внутри- и межпопуляционных отношений .

Нелинейная зависимость скорости размножения популяций жертв от плотности при малых значениях плотности (отсутствие достаточного количества брачных пар): A(u) = au2/(N + u), где a и N - положительные постоянные.

Внутривидовая конкуренция жертв: A(u) = au(l - u/K).

Насыщение хищников: Bi(u) = bu/(1 + au) - трофическая функция хищника.

Нелинейный характер выедания хищниками жертв: Bi(u) = bu2/(1 + au).

Конкуренция хищников за жертв: B2(v) = bv/(1 + |3v). При этом B(u,v) = = Bi(u)B2(v).

Конкуренция хищников за отличные от жертв ресурсы: C(v) = v/(1 + v/Ki).

Нелинейный характер зависимости скорости размножения хищника от плотности популяции при малых значениях плотности: C2(v) = cv/(Nv + v), при этом C(u,v) = C1(u)C2(v) и C1(u) = B1(u), D2(v) = cv, то есть C(u,v) = = cv/(Nv + v) Bi(u).

1. Математическая модель взаимодействия загрязнения с окружающей средой, трактуемая как модель «хищник-жертва»

Ситуацию «загрязнение-природа» можно трактовать как частный случай модели «хищник-жертва», когда природа выступает в качестве жертвы, а загрязнение -хищника. Главное предположение, лежащее в основе модели, состоит в том, что окружающая среда активно абсорбирует и перерабатывает загрязнение вплоть до определенного предела.

Из качественных соображений в системе окружающая среда - загрязнение возможны три следующих принципиально различных сценария взаимодействия.

1. При малых выбросах загрязнения окружающая среда его полностью перерабатывает (устойчивая ситуация).

2. При увеличении выбросов загрязнения в зависимости от внешних условий и случайных причин окружающая среда может находиться в удовлетворительном состоянии, а может и погибнуть (бистабильная ситуация)*.

3. Наконец, третья ситуация соответствует экологической катастрофе - полному вымиранию природы.

Предположим, что общий фон загрязнения и состояние окружающей среды можно характеризовать следующими переменными: концентрацией загрязнения P и плотностью биомассы E, соответственно. В том случае, если существует постоянно действующий источник загрязнения, процесс эволюции загрязнения можно описать уравнением

где a - мощность источника загрязнения за единицу времени, b - коэффициент естественного уничтожения загрязнения (такое уничтожение называют «мертвым», или

‘Бистабильная ситуация может реализоваться, когда в окрестности некоторых предприятий растительный покров остается только местами. Это следует из наблюдений и может служить во многом запоздалым сигналом для принятия срочных мер по спасению природы.

естественной диссипацией). При начальном условии P(t = 0) = Po решение уравнения (8) имеет вид:

P (t) = b+(Po - D e~bt’

то есть со временем концентрация загрязнения уменьшается естественным образом.

Предположим далее, что загрязнение находится в постоянном взаимодействии с окружающей средой, которая оказывает очищающий эффект на загрязнение. Будем также считать систему «окружающая среда - загрязнение» замкнутой. Тогда процесс взаимодействия с окружающей средой можно описать следующей системой уравнений:

J- = a - bP- f (E, P), - = g(E) - h(E, P), (9)

где функция f (E, P) > 0 - описывает абсорбирование и переработку загрязнения окружающей средой; g(E) - слагаемое, описывающее динамику окружающей среды в отсутствие загрязнения; h(E, P) - функция, описывающая вредное влияние загрязнения на окружающую среду.

Примем в качестве функций взаимодействия загрязнения и живой природы f (E, P) = cEP и h(E, P) = dEP, где c и d - постоянные коэффициенты.

Будем считать, что при отсутствии загрязнения поведение окружающей среды можно описать логистическим уравнением, то есть g(E) = rE(1 - E/К), где r - постоянный коэффициент, а К - соответствует максимальному значению E при dE/dt = 0. Подставив выражения для f (E, P), h(E, P), и g(E) в систему уравнений (9), получим

^ = a - bP- cEP, = rE (l -E) - dEP.

Переходя в системе уравнений (10) к безразмерным переменным

Т = bt, a = -pr, uo

получаем простейшую математическую модель взаимодействия загрязнения с окружающей средой в виде следующих уравнений:

A - u - uv, dt

v(u0 - u) - pv2.

Легко видеть, что система уравнений (10) есть система хищник-жертва, где в качестве жертвы выступает загрязнение (не биологический объект), а в качестве хищника - биологически активная окружающая среда.

В системе уравнений (11) параметр а можно трактовать как обобщенную мощность источника загрязнения; uo - предельно допустимая концентрация для данной экосистемы (если u > u0, dv/dt < 0, и природа вымирает); p - характеристика экосистемы - коэффициент внутривидовой конкуренции природы.

Положения равновесия системы уравнений (11), соответствующие условиям du/dt = 0 и dv/dt = 0, нетрудно найти из уравнений

а - u(l + v) = 0, -v(u - uo) - pv2 = 0.

Тогда Ai = (а, 0); A2 ((uo + p + Q)/2, (uo - p - Q)/(2p));

A3 ((uo + p - Q)/2, (uo - p + Q)/(2p)), Q = ^/(uo + p)2 - 4ap.

Второе и третье положения равновесия существуют, если [(u + p)2-4aP]>0. Стандартный линейный анализ на устойчивость указанных положений равновесия приводит к параметрическому портрету системы уравнений (11), приведенному на рис. 3. На рис. 4 приведены соответствующие фазовые портреты системы уравнений (11).

Если параметры принадлежат области IV, то все траектории за исключением устойчивого многообразия Ai стремятся при t ^ ж к A3 (рис. 4, а). Области II соответствует фазовый портрет на рис. 4, б. В области III существует единственный глобальный аттрактор A1 (рис. 4, в).

Таким образом, описанная математическая модель соответствует трем качественно описанным выше ситуациям.

Однако в начале этого раздела в качестве главного предположения было указано, что модель содержит пороговую величину загрязнения, которое способна переработать природа. Этот эффект нужно учесть в математической модели.

Рис. 3. Параметрический портрет системы уравнений (11). При фиксированном и0 вся область допустимых параметров разбивается на четыре множества

Для этого в книге предлагается использовать одну из трофических функций, описывающих процесс насыщения, например,

Тогда при малой концентрации загрязнения f (E, P) ~ cPE, при высокой концентрации f (E, P) cE, что более реалистично, чем первоначальное выражение.

После приведения системы уравнений (9) к безразмерному виду с учетом соотношения (12) и переобозначений в получена следующая система уравнений:

А - u ---, - = v(uo - u) - pv , dt к + u dt

где к = A(d/b) > 0 описывает степень влияния природы на загрязнение: чем больше его величина, тем меньше степень поглощения живой природы и наоборот.

В книге также указано, что в системе уравнений (13) возможны одно, два или три состояния равновесия такого же характера, как и для системы (11). Причем авторы подчеркивают, что априорные предположения относительно выбора тех или иных функциональных зависимостей в этой модели в большей степени адекватны действительности, чем выбранные модели (11).

2. Математическая модель очистки сточных вод

Будем рассматривать загрязнитель как «жертву», а биологически активный ил как «хищника». Процесс биохимического окисления загрязнителя будем трактовать как «поедание» его микроорганизмами активного ила.

Предположим, что имеется постоянный источник загрязнения, а активный ил способен перерабатывать загрязнение до определенного предела. Считаем, что изменение концентрации активного ила в чистой воде убывает по экспоненциальному закону.

Тогда динамику очистки сточных вод можно описать уравнениями

dd _ = а - bD(P) - cf (P, E), - = -dS + eh(P, E),

где P (t) - концентрация загрязнения воды, E (t) - плотность биомассы активного ила, D(P) - функция диссипации, характеризующая естественный распад загрязнения; f (P, E) и h(P, E) - трофические функции, характеризующие процесс очистки загрязнителя биологически чистым илом; a > 0 - мощность источника загрязнения; d > 0 - постоянная, характеризующая скорость убывания активного ила в чистой воде; c и e - положительные постоянные.

Допустим, что D(P) = P, а трофические функции «хищника» и «жертвы» одинаковы и имеют вид:

f (P, E) = h(P, E) = , где r > 0 - постоянная.

Тогда будем иметь:

A - bP--------, -

После введения безразмерных переменных т = at, P = ru(x), E = (rd/c) v(x) система уравнений (14) принимает вид

где a = a/(rd), в = b/d, у = e/d. Неподвижные точки системы (15) Ai(ui,vi) =

= (a/fr 0) и A2(u2, v2) = (1/(Y - 1), Hy - 1) - p]y/(y - 1)).

Стандартный линейный анализ показывает, что точка Ai(ui, vi) является седловой при в < a(Y - 1) и y > 0 и устойчивым узлом при в > a(Y - 1).

Если увеличивать значение параметра a при фиксированных значениях в и (Y - 1), что соответствует увеличению интенсивности источника загрязнения, то возникает устойчивое состояние равновесия A^(u2,v2). Если параметр a мал (мала интенсивность загрязнения), то масса биологически активного ила стремится к нулю. Поскольку загрязнитель является пищей для биологически активного ила, при недостаточной интенсивности загрязнителя биологически активный ил исчезает.

Разумно предположить, что существует некоторое пороговое значение концентрации загрязнения P *, при превышении которого очищающая способность ила уменьшается, и рассмотреть трофические функции вида

f (P, E) = EPe-rP, r = const > 0.

В этом случае величина порогового значения загрязнения P* = 1/r. В реальности в описываемом процессе есть еще одна компонента - процесс аэрации - насыщения ила кислородом, который значительно повышает способность переработки биологически активным илом загрязнителя. С учетом сказанного математическая модель очистки примет вид:

a - bP - cf (P, E),

dE + ef (P, E)Q(t),

где a, b, c,d,e = const > 0. Здесь Q(t) - концентрация кислорода, а R> 0 определяет величину притока кислорода в систему в единицу времени.

Проведенный авторами книги анализ системы уравнений (16) в предположении, что f (P, E) = Pg(E), где g(E) - гладкая монотонно возрастающая неотрицательная функция (причем g(0) = 0), показывает, что при достаточно близких значениях параметра R, определяющего количество поступающего в систему кислорода, всегда можно добиться стабильности системы.

3. Моделирование классовой борьбы

Запишем уравнения модели «хищник-жертва» в виде следующей системы:

где x, у - численность популяций, x1 и у1 - их стационарные значения, а и b -постоянные.

Эта модель используется для описания малых городских ареалов . В этом случае переменная x в системе уравнений (17) означает площадь землепользования, у - земельную ренту, a, b, xi, yi - некоторые параметры.

Интересное приложение модели для описания классовой борьбы дано Гудвином . Рассмотрим, следуя , два типа граждан: рабочих и капиталистов.

Рабочие тратят весь свой доход wL на потребление, капиталисты накапливают свой доход Y - wL, где Y - продукция производства. Цена потребительских товаров нормирована к единице.

Пусть K означает капитал, а = ао egt = Y/L - производительность труда, возрастающую с постоянной скоростью д, к = K/Y - коэффициент капиталоемкости продукции, N = Noent - предложение на рынке рабочей силы, которое увеличивается с темпом роста п. Доля затрат на оплату труда по отношению к национальному доходу составляет wL/Y = w/a. Следовательно, доля прибыли капиталистов составляет (1 - w/a). Поскольку сбережения можно определить как S = Y - wL = (1 - w/a)Y, доля инвестиций составляет dK/dt = S = (1 - w/a)Y или (dK/dt)(1/K) = (1 - w/a)(Y/K); при этом выбытием капитала пренебрегаем.

При постоянном значении капиталоемкости к = K/Y получаем dk/dt = 0 и

dY dL 1 dt Y dt L

Кроме того, из (18) с учетом того, что dK/dt = (1 - w/a)L, следует

dY 1 dK 1 / w \ 1

dt Y dt K V a) k-

Из соотношений (19) и (20) окончательно находим:

Введем новые переменные: y = w/a - доля затрат на оплату труда; x = L/N -коэффициент занятости.

После простых преобразований, с учетом (21) получаем

dx - = x dt 1 - у к (д + п)

dt =у w dt a dt

Wf (х), lim f (x) dt

lim f (x) < 0,

Линейная аппроксимация f (x) в виде (dw/dt)(l/w) = -r + bx превращает (23) в следующее уравнение:

R + px - g. (24)

Объединяя (22) и уравнений

(24), приходим к модели Гудвина, описываемой системой

y[-(g + r) + px}.

Очевидно, что система уравнений (25) эквивалентна системе уравнений (17), поэтому все выводы общего характера, справедливые для системы (17), верны и для модели Гудвина.

Заметим, что модель Гудвина, учитывающая взаимодействие между уровнем занятости и законодательно установленной долей отчислений на оплату труда, весьма напоминает классические модели политической экономии (её иногда называют неомарксистской). Модель вновь привлекает внимание к трудам экономистов-классиков, таких как Риккардо, Смит, Маркс. Увы, модель структурно неустойчива.

Итак, модель «хищник»-«жертва» может быть использована для моделирования явлений взаимосвязи городской земельной ренты и интенсивности землепользования, безработицы и динамики экономического роста.

4. Модель «хищник-жертва» для описания бесклассового общества -общества эпохи охотников-собирателей

Для этой эпохи характерна низкая плотность населения и общинная (родовая) организация человеческого сообщества. Человек полностью зависел от природы, шла постоянная борьба за выживание, а главным из добываемых ресурсов была пища. Человек был частью экосистемы и отличался от других стайных хищников, по-существу, лишь умением использовать для собственных нужд огонь и примитивные орудия труда. Изменение численности населения в конкретном ареале, в основном, определялось состоянием ресурсной базы и может быть описано моделью «хищник-жертва» - системой уравнений (1). Теперь в этих уравнениях N - численность популяции объектов охоты («жертв»); P - численность древних охотников («хищников») в рассматриваемом ареале; cNP - скорость рождения «хищников»; dP - смертность «хищников»; aN - скорость гибели «жертв» (считается, что их пищевая база неограниченна); bNP - скорость гибели «жертв» за счет их истребления «хищниками» (считается, что это единственная причина смертности «жертв». Решения этих уравнений анализировались во Введении). Поскольку охотники-собиратели потребляли то, что было произведено в природе без их участия, численность популяции определялась внешними условиями, повлиять на которые они не могли (в модели численность охотников-собирателей колеблется около среднего значения

Po = a/b. Заметим, что именно этим объясняется относительная стабильность численности населения Земли на протяжении всего каменного века до эпохи неолита.

Когда человек приручил животных и научился возделывать культурные растения, он превратился из охотника-собирателя в скотовода и земледельца. Таким образом, значительно увеличился коэффициент а и равновесная численность людей, поскольку величина коэффициента b, характеризующего потребление, осталась примерно на прежнем уровне.

5. Сходная идеология людей для описания военных действий

В книге Фредерик Ланчестер - английский эрудит и инженер - предложил простую модель борьбы двух противников (скажем, двух армий), которая носит его имя. Заметим, что такая же модель была предложена офицером царской армии М.О. Осиповым в 1915 году . Поэтому справедливо называть эту модель моделью Ланчестера-Осипова. Далее в изложении будем следовать работе . В данной модели состояние системы описывается точкой (x, у) положительного квадранта плоскости. Координаты этой точки x и у - численности противостоящих армий. Уравнения модели имеют следующий вид:

By, - = -ax. (26)

Здесь а и b - мощность оружия армии x и армии у, соответственно. Другими словами, каждый солдат армии x убивает за единицу времени а солдат армии у (и соответственно каждый солдат армии у убивает b солдат армии x). Таким образом, общая эффективность всех выстрелов армии x дается как ax, а для армии у - как by. В работе предполагается, что непрерывная аппроксимация достаточно хороша, и скорость изменения численности войск пропорциональна эффективности выстрелов противной стороны. «Жесткая», по В.И. Арнольду, модель (26) допускает точное решение в виде:

ax2 - Ьу2 = const. (27)

Изменение численности армий x и у происходит вдоль гиперболы, заданной уравнением (27) (рис. 5). По какой именно гиперболе пойдет война, зависит от начальной точки. Гиперболы разделены прямой л/ax = \[Ъу. Если начальная точка лежит выше этой прямой, то гипербола выходит на ось у. Это означает, что в ходе войны численность армии x уменьшается за конечное время до нуля. Армия у выигрывает, противник уничтожен. Если же начальная точка лежит ниже прямой, выигрывает армия х. На прямой, как пишет Арнольд, война «к всеобщему удовлетворению» заканчивается истреблением обеих армий. Но на это требуется бесконечно большое время: конфликт продолжает тлеть, когда оба противника уже обессилены. Из соотношения (27) следует, что на прямой ^fax = -\[Ъу. Тогда первое уравнение системы (26) принимает вид: dx/dt =

Y/abx. Его решением является x = Ce~^a>t, где

С = и очевидно, что x > 0 при t > Ж. Рис. 5. «Жесткая» модель войны

Рис. 6. «Мягкая» модель войны

Из модели (26) следует вывод, что для борьбы с вдвое более многочисленным противником необходимо иметь в четыре раза более мощное оружие, с втрое более многочисленным - в девять раз и т.д. На это указывают квадратные корни в уравнении прямой.

Ясно, что получившаяся, в терминологии Арнольда, «людоедская» модель сильно идеализирована, и её опасно применять к реальной ситуации. Что изменится, если

Эта система уравнений уже не решается в явном виде. Но модель за счет изменений a(x, у) и b(x, у) становится «мягкой». Кривые на плоскости (x, у) уже не гиперболы и разделяет их не прямая (рис. 6). Но основной качественный вывод остается прежним: ситуации «x выигрывает» и «у выигрывает» разделены нейтральной линией «обе армии уничтожают друг друга за бесконечное время».

6. Простейшая вирусная модель инфекционного заболевания

В 1974 году Г. Белл предложил простейшую модель иммунной реакции, в которой взаимодействие между антигеном и антителом описывается в терминах «хищник-жертва».

Изложим вариант теории Г. Белла , исходя из более общей модели Г.И. Марчука .

Основными факторами в модели инфекционного заболевания являются следующие:

Концентрация патогенных размножающихся антигенов V (t);

Концентрация антител F(t); под антителами понимают субстраты иммунной

системы, нейтрализующие антигены (иммуноглобулины, рецепторы клеток);

Концентрация плазмоклеток C - носителей и продуцентов антител - предполагается постоянной;

Степень поражения органа-мишени не учитывается.

Уравнение, описывающее изменение числа антигенов (чужеродных клеток, проникающих в организм), имеет вид

W = eV - YFV (28)

Первое слагаемое в уравнении (28) - скорость прироста антигенов за счет размножения; в - коэффициент размножения антигенов; слагаемое yFV описывает число антигенов, нейтрализуемых антителами F в единицу времени; у - коэффициент, связанный с вероятностью нейтрализации антигена антителами при встрече с ними.

Для получения второго уравнения подсчитаем баланс числа антител, реагирующих с антигеном. Будем иметь

dF = pCdt - nyFVdt - ц/Fdt. (29)

Первое слагаемое в правой части уравнения (29) описывает генерацию антител плазменными клетками за время dt; р - скорость производства антител плазмоклеткой. Второе слагаемое (nyFVdt) описывает уменьшение числа антител за счет связи с антигенами, причем на нейтрализацию одного антигена приходится п антител. Третье слагаемое (ifFdt) описывает уменьшение популяции антител за счет старения; if - коэффициент, обратно пропорциональный времени распада антител. Разделив уравнение (29) на dt, получим

РС - (if + nyV)F. (30)

Если при t < to V(t) = 0, то начальные условия имеют вид

V (to) = Vo, F (to) = Fo. (31)

Пусть в дальнейшем to = 0.

Рассмотрим два предельных случая динамики болезни. Допустим, что организм не производит антител данной специфичности, то есть F(t) = Fo = 0 для всех t > 0 и р = 0. Тогда из (28) следует, что

- = |3V и V (t) = Voeet, (32)

где Vo - доза заражения (начальная концентрация антигенов) при t = 0. Очевидно, что такое решение соответствует течению болезни с летальным исходом, так как нет компенсирующих рост антигенов факторов. Второй предельный случай: присутствующие в организме антитела (специфические к данному антигену) достаточны для того, чтобы уничтожить все проникшие в организм антигены, не включая в действие механизм антителообразования. В этом случае в уравнении (28) в ^ yF. Предполагая дозу заражения Vo малой, можно считать величину F постоянной, определяемой нормальным уровнем антител F*. Тогда уравнение (28) имеет вид

Ж = (в - YF*> V

и его решение записывается так:

V = Voe-(YF *-e)t.

В предельном случае, когда B = 0

V = Voe-YF ч, (33)

что соответствует высокому иммунологическому барьеру.

Решения (32) и (33) представлены на рис. 7.

При заданных значениях коэффициентов модели и начальных условиях и естественно, что все семейство разнообразных динамик заболевания уложится в заштрихованной области на рис. 7 .

ниченная решениями для двух предельных случаев

7. Сходные модели распространения эпидемий

Рассмотрим SIR-модель Кермака-МакКендрика, полагая, что особи популяции могут быть в трех различных состояниях:

S (t) - здоровые особи, которые находятся в группе риска и могут подхватить инфекцию;

I(t) - заразившиеся переносчики болезни;

R(t) - те, кто выздоровел и перестал распространять болезнь (в эту категорию относят, например, приобретших иммунитет или даже умерших).

Типичная эволюция особи популяции описывается следующей диаграммой:

Построим феноменологическую модель, соответствующую диаграмме, используя следующие допущения:

1) популяция замкнута и имеет постоянный размер N;

2) промежуток времени, когда заболевший остается опасным для окружающих, распределен по экспоненциальному закону со средним 1/у;

3) контакты случайны и равновозможны (однородное перемешивание).

При этих допущениях будем иметь:

где X - так называемая сила инфекции, которая в данном случае равна произведению количества контактов в единицу времени, сделанных одним здоровым (обозначим это количество как cN), вероятности передать ему инфекцию при контакте p и вероятности встретить заболевшего I(t) /N. Обозначим в = cp. Тогда получаем X = |3! и приходим к стандартной форме уравнений:

w dt = S-■<’" ~dt = -о* d + d. + dt = 0и

S (t) + I (t) + R(t) = N.

Третье уравнение в приведенной системе избыточно и, поскольку dS/dt < 0, то естественно считать фазовым пространством треугольник S(t) + I(t) < N.

Из первого и второго уравнений системы (34) следует, что

dL =(М-Т^ = -1+ о о = Y I = о dS eSI S’ о в, I =

Учитывая начальные условия S(0) = So, I(0) = I0, найдем первый интеграл I + S - о ln S = I0 + S0 - о ln S0, с помощью которого можно построить фазовые кривые на плоскости (S, I) (рис. 8). Кривые, приведенные на рис. 8, б, хорошо совпадают с данными по эпидемии чумы в Бомбее 1906 года.

В книге предложено использовать модель, рассмотренную выше, с некоторой модификацией для анализа заражения вирусом компьютеров. Постановка задачи следующая.

Пусть S - число компьютеров, которые подвергаются заражению вирусом, I - часть компьютеров, зараженных вирусом и не имеющих антивирусного программного обеспечения, R - часть компьютеров, имеющих должную антивирусную защиту (иммунитет). Тогда уравнения модели имеют вид (см. систему уравнений (34)):

^ = -aSI, ^ = aSI - bI, ^ = bI. dt dt dt

Основная идея модификации этой классической модели эпидемии состоит во введении элемента цикличности, то есть элемента регулирующего добавления новых подверженных эпидемии компьютеров. В каждый новый отрезок времени число инфицированных компьютеров вычисляется на основе количества инфицированных компьютеров, оставшихся от предыдущего момента, а число подверженных эпидемии компьютеров разыгрывается как случайная величина по закону Пуассона с распределением pm = (Xm/m\)e-x, m = 1,2,...

Решение задачи в не приводится. Авторы предлагают следующий путь решения. Построить график функции I(t), численно решая приведенную выше систему уравнений с начальными условиями 5(0) = 100, I(0) = 1, R(0) = 0, X = 10, a = 0.23, b = 0.5. Добавление новых элементов предлагается производить при tk = к, к = 1, 2, ...100.

Возможно, кого-то из читателей заинтересует решение этой задачи и её многочисленных вариантов.

8. Обобщенная модель Лотки-Вольтерры для описания

взаимодействия когнитивных и/или эмоциональных мод мозга

Согласно работе , крупномасштабные когнитивные паттерны (моды или представления, наблюдаемые в эксперименте) в рабочем режиме мозга должны подавлять друг друга, что естественно должно происходить последовательно во времени. Иными словами, работающий мозг демонстрирует когнитивную и эмоциональную активность в виде цепочки сменяющих друг друга во времени комбинаций функциональных мод, а сами эти комбинации определяются родом ментальной активности.

По мнению авторов , «...конкуренция за конечные ресурсы одна из главных действующих сил, управляющих процессами мозга. Эти ресурсы - энергия (кислород и глюкоза) и информация (внимание и память). Важно, что информационные ресурсы -продукт деятельности самого мозга, то есть они могут по-разному влиять на эмоции и когнитивные функции (например, за счет управления вниманием) и должны Быть включены в общую динамическую модель, определяющую рабочее пространство. ...Моды, представляющие в рабочем пространстве эмоции и когнитивные функции, взаимно обмениваются информацией и конкурируют в борьбе за энергетические и информационные ресурсы».

функционально определяемым взаимодействием различных подсистем мозга, их конкуренцией и синхронизацией (координацией) во времени». Упомянутые выше процессы конкуренции когнитивных и эмоциональных мод между собой, а также эмоциональных и когнитивных мод друг с другом в работе предлагается описывать системами уравнений типа Лотки-Вольтерры в следующей обобщенной форме:

Vi(E) -^2 Wi,j(E)xi(t)

Здесь Xi(t) характеризует активность i-й моды (численность i-й популяции в экологии); n - число взаимодействующих мод (популяций); щ(Е) - поступающая в систему информация или доступные ресурсы; ф^- (E) - элементы матрицы взаимодействия; n(t) - мультипликативный шум, присутствующий в системе; т - характерное время, определяющее процесс.

Если учесть специфику ресурсов, за которые борются когнитивные и эмоциональные моды, подсистем уравнений (36) должно быть три: моды эмоций, когнитивные моды и ресурсы (внимание, память, энергия). Особенно велика роль внимания. В статье для простоты считается, ...что описание конкуренции за внимание между эмоциями и когнитивными функциями не требует спецификации отдельных мод, и поэтому можно ограничиться рассмотрением конкурентной борьбы за внимание «в целом» эмоций B = ^П=1 Bi и «в целом» когнитивных мод A = ^П=1 Ai. Тогда базовые уравнения можно записать в виде:

Oi(I,B,D)Ra -^2 Pij(D)Aj(t)

Zi(S, A,D)Rb -£ lij (D)Bj(t)

Ai(t)n(t), i = 1,...N,

Bi(t)n(t), i = 1, ...M,

RA(t) A - (RA(t) + Фл(1, D)Rb(t)) = Rb(t) B - (Rb(t) + Фв(S, D)RA(t))

В этих уравнениях Ai и Bi - неотрицательные переменные, соответствующие когнитивным и эмоциональным модам, общая интенсивность которых обозначается A и В, соответственно; I - информация от внешнего мира; S - характеристика эмоционального влияния от внешнего мира (в случае отрицательных эмоций - стресс); D -уровень принимаемых лекарств; та и тв - характерные времена сознательной и эмоциональной активностей; n(t) - мультипликативный шум; коэффициенты Фа и Фв определяют интенсивность борьбы за внимание со стороны эмоций и мышления. Зависимость параметров Oi и Zi от A и B, соответственно, описывает прямое влияние активности когнитивных процессов на эмоции и эмоций на мышление. В статье

представлен компьютерный анализ выписанных выше уравнений при наличии внешнего стимула S(t), характеризующего уровень стресса. Обсуждается также взаимодействие настроения и мышления. Анализируется взаимодействие трех компонент активности мозга: поведения, эмоциональной памяти и когнитивной деятельности при отсутствии внешних воздействий.

Вместо заключения

В замечательной книге Ю.И. Неймарка есть такие слова.

«Что такое модель? Слово “модель” из итальянского языка и означает “копия, образец, прототип”, изучив который, мы познаем оригинал. Значит, математическая модель - это прототип какой-то части мира - объекта, системы, устройства, машины, процесса, прибора, изучая который, мы постигаем эту часть мира...»

Если модель типовая (см. эпиграф) или, как говорят, эталонная, то с её помощью можно постичь не одну, а разные части мира. Именно такой моделью является математическая модель Лотки-Вольтерры. Разумеется, представленный обзор охватывает только часть её возможных приложений и не претендует на всеобщность.

Библиографический список

1. Ch. Darvin. Autobiography. 1958. C. 120.

2. Браун Джанет. Чарльз Дарвин. Происхождение видов / Сер. «10 книг, изменивших мир». М.: АСТ: аст., 2009. 220 с.

3. Malthus T.R. An assay on the principle of population, as it affects the future improvement of society. 1798.

http://www.faculty.rsu.edu/ felwell/Theorists/Malthus/essay2.htm

4. Lotka A. Elements of Physical Biology. Baltimore, 1925. Reprinted by Dover in 1956 as Elements of Mathematical Biology.

5. Вольтерра В. Математическая теория борьбы за существование / Пер. с франц. М.: Наука, Главная редакция физико-математической литературы, 1976. 288 с.

6. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии. М.: ФИЗМАТЛИТ, 2010. 400 с.

7. Базыкин А.Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных исследований, 2003. 368 с.

8. Арнольд В.И. «Жесткие» и «мягкие» модели // Природа. 1998. № 4. С. 3.

9. Братусь А.С., Мещерин А.С., Новожилов А.С. Математические модели взаимодействия загрязнения с окружающей средой // Вестник МГУ. Сер. Вычислительная математика и кибернетика. 2001. Т. 6. С. 140.

10. Занг В.-Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории / Пер. с англ. М.: Мир, 1999. 335 с.

11. Goodwin R.M. A Growth Model // Socialism and Growth. Cambridge: University Press, 1967.

12. Малков С.Ю. Социальная самоорганизация и исторический процесс. Глава 2. М.: УРСС, 2009.

13. Lanchester F W. Aircraft in warfire: The down of the fourth arm. London, Constable, 1916.

14. Осипов М.О. О влиянии численности вступающих в бой сил на их потери // Военный сборник, июнь-октябрь, 1915.

15. Bell G. Prey - predator equations simulating on immune response // Math. Biosci. 1973. № 16. C. 291.

16. Марчук Г.И. Математические модели в иммунологии и медицине. Глава 2. М.: Наука, 1985.

17. Kermack W.O. and Mc.Kendrick A.G. Contribution to the mathematical theory of epidemics // Proceedings of Royal Statistical Society A. 1927. Vol. 115. P. 700.

18. Рабинович М.И., Мюезинолу М.К. Нелинейная динамика мозга: эмоции и интеллектуальная деятельность // УФН. 2010. № 4.

19. Неймарк Ю.И. Математические модели в естествознании и технике. Н. Новгород: Издательство Нижегородского университета, 2004.

Саратовский государственный Поступила в редакцию 11.02.2011

университет им. Н.Г. Чернышевского

PHENOMENON OF LOTKA-VOLTERRA MATHEMATICAL MODEL

AND SIMILAR MODELS

Lotka-Volterra mathematical model (often called «predator-prey» model) is applicable for different processes description in biology, ecology, medicine, in sociology investigations, in history, radiophysics, ets.

Variants of this model is considered methodologicaly in this review.

The next models are observed: model of contamination or other dirty interaction with surroundigs; model of class struggle; model of classless society - epock of hunters-gatherers; military operations model; model of virus infection diseases; model of epidemic spreading, so virus of computers infection spreading; model of cognitive and(or) emotion cerebral modes.

Keywords: Lotka-Volterra mathematical model, «predator-prey» system, analysis of natural or society phenomena.

Трубецков Дмитрий Иванович - родился в Саратове (1938). Окончил физический факультет Саратовского государственного университета (1960). Защитил диссертации на соискание ученой степени кандидата (1965) и доктора физико-математических наук в СГУ (1978) в области радиофизики. Заведующий кафедрой электроники, колебаний и волн факультета нелинейных процессов СГУ, профессор, член-корреспондент Российской академии наук, заслуженный деятель науки РФ, лауреат премии Президента РФ в области образования. Научный руководитель Лицея прикладных наук и факультета нелинейных процессов СГУ Область научных интересов: вакуумная электроника и микроэлектроника сверхвысоких частот, теория колебаний и волн, нелинейная динамика, история науки. Автор более двадцати учебных пособий и монографий, а также более двухсот статей в периодической печати.

410012, Саратов, ул. Астраханская, 83

Саратовский государственный университет им. Н.Г. Чернышевского E-mail: [email protected]

Еще в 20-х гг. А. Лотка, а несколько позднее независимо от него В.Вольтера предложили математические модели, описывающие сопряженные колебания численности хищника и жертвы.

Модель состоит из двух компонентов:

С – численность хищников; N – численность жертв;

Предположим, что в отсутствии хищников популяция жертвы будет расти экспоненциально: dN/dt = rN. Но жертвы уничтожаются хищниками со скоростью, которая определяется частотой встреч хищника с жертвой, а частота встреч возрастает по мере увеличения численности хищника (С) и жертвы (N). Точное число встреченных и успешно съеденных жертв будет зависеть от эффективности, с которой хищник находит и ловит жертву, т.е. от а’ – «эффективности поиска» или «частоты нападений». Т.о., частота «успешных» встреч хищника с жертвой и, следовательно, скорость поедания жертв будет равна а’СN и в целом: dN/dt = rN – a’CN (1*).

В отсутствии пищи отдельные особи хищника теряют в весе, голодают и гибнут. Предположим, что в рассматриваемой модели численность популяции хищника в отсутствии пищи вследствие голодания будет уменьшаться экспоненциально: dC/dt = - qC, где q – смертность. Гибель компенсируется рождением новых особей со скоростью, которая, как полагают в этой модели, зависит от двух обстоятельств:

1) скорости потребления пищи, a’CN;

2)эффективности (f), с которой эта пища переходит в потомство хищника.

Т.о., рождаемость хищника равна fa’CN и в целом: dC/dt = fa’CN – qC (2*). Уравнения 1* и 2* составляют модель Лотки-Вольтера. Свойства этой модели можно исследовать, построить изоклины линии, соответствующие постоянной численности популяции, с помощью таких изоклин определяют поведение взаимодействующих популяций хищник-жертва.

В случае с популяцией жертвы: dN/dt = 0, rN = a’CN, или C = r/a’. Т.к. r и a’ = const, изоклиной для жертвы будет линия, для которой величина С является постоянной:

При низкой плотности хищника (С), численность жертвы (N) возрастает, наоборот – снижается.

Точно также для хищников (уравнение 2*) при dC/dt = 0, fa’CN = qC, или N = q/fa’, т.е. изоклиной для хищника будет линия, вдоль которой N постоянна: При высокой плотности жертвы, численность популяции хищника растет, а при низкой – снижается.

Их численность претерпевает неограниченные сопряженные колебания. Когда велико число жертв, численность хищников растет, что приводит к увеличению пресса хищников на популяцию жертвы и тем самым к уменьшению ее численности. Это снижение в свою очередь ведет к ограничению хищников в пище и падению их численности, которая вызывает ослабление пресса хищников и увеличение численности жертвы, что снова приводит к росту популяции хищников и т.д.

Популяции неограниченно долго совершают один и тот же цикл колебаний до тех пор, пока какое-либо внешнее воздействие не изменит их численность, после чего популяции совершают новые циклы неограниченных колебаний. На самом деле среда постоянно меняется, и численность популяций будет постоянно смещаться на новый уровень. Чтобы циклы колебаний, которые совершает популяция, были регулярными, они должны быть стабильными: если внешнее воздействие изменяет уровень численности популяций, то они должны стремиться к первоначальному циклу. Такие циклы называются устойчивыми, предельными циклами.

Модель Лотки-Вольтера позволяет показать основную тенденцию в отношениях хищник-жертва, которая выражается в возникновении колебаний численности в популяции жертвы, сопровождающихся колебаниями численности в популяции хищника. Основным механизмом таких колебаний является запаздывание во времени, свойственное последовательности состояния от высокой численности жертв к высокой численности хищников, затем к низкой численности жертв и низкой численности хищников, к высокой численности жертв и т.д.

5) ПОПУЛЯЦИОННЫЕ СТРАТЕГИИ ХИЩНИКА И ЖЕРТВЫ

Взаимоотношения «хищник - жертва» представляют звенья процесса передачи вещества и энергии от фитофагов к зоофагам или от хищников низшего порядка к хищникам высшего порядка. По характеру этих отношений различают три варианта хищников :

а) собиратели . Хищник собирает мелких достаточно многочисленных подвижных жертв. Такой вариант хищничества характерен для многих видов птиц (ржанок, зябликов, коньков и др.), которые затрачивают энергию только на поиск жертв;

б) истинные хищники . Хищник преследует и убивает жертву;

в) пастбищники . Эти хищники используют жертву многократно, например, оводы или слепни.

Стратегия добывания пищи у хищников направлена на обеспечение энергетической эффективности питания: затраты энергии на добывание пищи должны быть меньше энергии, получаемой при ее усвоении.

Истинные хищники делятся на

«жнецов», которые питаются обильными ресурсами (н, планктонные рыбы и даже усатый кит), и «охотников», которые добывают менее обильный корм. В свою очередь

«охотники» делятся на «засадников», подстерегающих добычу (например, щука, ястреб, кошка, жук- богомол), «искателей» (насекомоядные птицы) и «преследователей». Для последней группы поиск пищи не требует больших затрат энергии, но ее нужно много, чтобы овладеть жертвой (львы в саваннах). Впрочем, некоторые хищники могут сочетать элементы стратегии разных вариантов охоты.

Как и при отношениях «фитофаг - растение», ситуация, при которой все жертвы будут съедены хищниками, что в конечном итоге приведет и к их гибели, в природе не наблюдается. Экологическое равновесие между хищниками и жертвами поддерживается специальными механизмами , снижающими риск полного истребления жертв. Так, жертвы могут :

Убегать от хищника. В этом случае в результате адаптаций повышается подвижность и жертв, и хищников, что особенно характерно для степных животных, которым негде прятаться от преследователей;

Приобретать защитную окраску («притворяться» листьями или сучками) или, напротив, яркий цвет, Н.: красный, предупреждающий хищника о горьком вкусе. Общеизвестно изменение окраски зайца в разные времена года, что позволяет ему маскироваться летом в траве, а зимой на фоне белого снега. Адаптивное изменение окраски может происходить в разных стадиях онтогенеза: детеныши тюленей белые (цвет снега), а взрослые особи черные (цвет скалистого побережья);

Распространяться группами, что делает их поиск и промысел для хищника более энергоемким;

Прятаться в укрытия;

Переходить к мерам активной обороны (травоядные, имеющие рога, колючие рыбы), иногда совместной (овцебыки могут занимать «круговую оборону» от волков и т.д.).

В свою очередь хищники развивают не только способность к быстрому преследованию жертв, но и обоняние, позволяющее по запаху определить место нахождения жертвы. Многие виды хищников разрывают норы своих жертв (лисы, волки).

В то же время сами они делают все возможное для того, чтобы не обнаружить своего присутствия. Этим объясняется чистоплотность мелких кошачьих, которые для устранения запаха много времени тратят на туалет и закапывают экскременты. Хищники одевают «маскировочные халаты» (полосатость щук и окуней, делающих их менее заметными в зарослях макрофитов, полосатость тигров и т.д.).

Полной защиты от хищников всех особей в популяциях животных-жертв также не происходит, так как это привело бы не только к гибели голодающих хищников, но в конечном итоге - к катастрофе популяций жертв. В то же время при отсутствии или снижении плотности популяции хищников ухудшается генофонд популяции жертв (сохраняются больные и старые животные) и ввиду резкого увеличения их численности подрывается кормовая база.

По этой причине эффект зависимости численности популяций жертв и хищников - пульсация численности популяции жертвы, за которой с некоторым запаздыванием пульсирует численность популяции хищника («эффект Лотки - Вольтерры») - наблюдается редко.

Между биомассами хищников и жертв устанавливается достаточно устойчивое соотношение. Так, Р. Риклефс приводит данные о том, что соотношение биомасс хищника и жертвы колеблется в пределах 1:150 - 1:300. В разных экосистемах умеренной зоны США на одного волка приходится 300 мелких белохвостых оленей (вес 60 кг), 100 крупных оленей вапити (вес 300 кг) или 30 лосей (вес 350). Такая же закономерность выявлена в саваннах.

При интенсивной эксплуатации популяций фитофагов человек нередко исключает из экосистем хищников (в Великобритании, к примеру, есть косули и олени, но нет волков; в искусственных водоемах, где разводят карпа и другую прудовую рыбу, нет щук). В этом случае роль хищника выполняет сам человек, изымая часть особей популяции фитофага.

Особый вариант хищничества наблюдается у растений и грибов. В царстве растений встречается порядка 500 видов, способных ловить насекомых и частично их переваривать с помощью протеолитических ферментов. Хищные грибы образуют ловчие аппараты в виде маленьких овальных или шаровидных головок, расположенных на коротких веточках мицелия. Однако самый распространенный вид ловушки - клейкие трехмерные сети, состоящие из большого числа колец, образующихся в результате ветвления гиф. Хищные грибы могут ловить достаточно крупных животных, например, круглых червей. После того, как червь запутается в гифах, они прорастают внутрь тела животного и быстро его заполняют.

1.Постоянный и благоприятный уровень температуры и влажности.

2.Обилие пищи.

3.Защита от неблагоприятных факторов.

4.Агрессивный химический состав среды обитания (пищеварительные соки).

1.Наличие двух сред обитания: среда первого порядка - организм хозяина, среда второго порядка - внешняя среда.

Модели взаимодействия двух видов

Гипотезы Вольтерра. Аналогии с химической кинетикой. Вольтерровские модели взаимодействий. Классификация типов взаимодействий Конкуренция. Хищник-жертва. Обобщенные модели взаимодействия видов. Модель Колмогорова. Модель взаимодействия двух видов насекомых Макартура. Параметрический и фазовые портреты системы Базыкина.

Основателемсовременной математической теории популяций справедливо считается итальянский математик Вито Вольтерра, разработавший математическую теорию биологических сообществ, аппаратом которой служат дифференциальные и интегро-дифференциальные уравнения. (Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Paris , 1931). В последующие десятилетия популяционная динамика развивалась, в основном, в русле высказанных в этой книге идей. Русский перевод книги Вольтерра вышел в 1976 г. под названием: «Математическая теория борьбы за существование» с послесловием Ю.М. Свирежева, в котором рассматривается история развития математической экологии в период 1931‑1976 гг.

Книга Вольтерра написана так, как пишут книги по математике. В ней сначала сформулированы некоторые предположения о математических объектах, которые предполагается изучать, а затем проводится математическое исследование свойств этих объектов.

Системы, изученные Вольтерра, состоят их двух или нескольких видов. В отдельных случаях рассматривается запас используемой пищи. В основу уравнений, описывающих взаимодействие этих видов, положены следующие представления.

Гипотезы Вольтерра

1. Пища либо имеется в неограниченном количестве, либо ее поступление с течением времени жестко регламентировано.

2. Особи каждого вида отмирают так, что в единицу времени погибает постоянная доля существующих особей.

3. Хищные виды поедают жертв, причем в единицу времени количество съеденных жертв всегда пропорционально вероятности встречи особей этих двух видов, т.е. произведению количества хищников на количество жертв.

4. Если имеется пища в ограниченном количестве и несколько видов, которые способны ее потреблять, то доля пищи, потребляемой видом в единицу времени, пропорциональна количеству особей этого вида, взятому с некоторым коэффициентом, зависящим от вида (модели межвидовой конкуренции).

5. Если вид питается пищей, имеющейся в неограниченном количестве, прирост численности вида в единицу времени пропорционален численности вида.

6. Если вид питается пищей, имеющейся в ограниченном количестве, то его размножение регулируется скоростью потребления пищи, т.е. за единицу времени прирост пропорционален количеству съеденной пищи.

Аналогии с химической кинетикой

Эти гипотезы имеют близкие параллели с химической кинетикой. В уравнениях популяционной динамики, как и в уравнениях химической кинетики, используется “принцип соударений”, когда скорость реакции пропорциональна произведению концентраций реагирующих компонентов.

Действительно, согласно гипотезам Вольтерра, скорость процесса отмирания каждого вида пропорциональна численности вида. В химической кинетике это соответствует мономолекулярной реакции распада некоторого вещества, а в математической модели – отрицательным линейным членам в правых частях уравнений.

Согласно представлениям химической кинетики, скорость бимолекулярной реакции взаимодействия двух веществ пропорциональна вероятности столкновения этих веществ, т.е. произведению их концентрации. Точно так же, в соответствии с гипотезами Вольтерра, скорость размножения хищников (гибели жертв) пропорциональна вероятности встреч особей хищника и жертвы, т.е. произведению их численностей. И в том и в другом случае в модельной системе появляются билинейные члены в правых частях соответствующих уравнений.

Наконец, линейные положительные члены в правых частях уравнений Вольтерра, отвечающие росту популяций в неограниченных условиях, соответствуют автокаталитическим членам химических реакций. Такое сходство уравнений в химических и экологических моделях позволяет применить для математического моделирования кинетики популяций те же методы исследований, что и для систем химических реакций.

Классификация типов взаимодействий

В соответствии с гипотезами Вольтерра взаимодействие двух видов, численности которых x 1 иx 2 , могут быть описаны уравнениями:

(9.1)

Здесь параметры a i ‑ константы собственной скорости роста видов, c i ‑ константы самоограничения численности (внутривидовой конкуренции), b ij ‑ константы взаимодействия видов, (i , j= 1,2). Знаки этих коэффициентов определяют тип взаимодействия.

В биологической литературе обычно классифицируют взаимодействия по участвующим в них механизмам. Разнообразие здесь огромно: различные трофические взаимодействия, химические взаимодействия, существующие между бактериями и планктонными водорослями, взаимодействия грибов с другими организмами, сукцессии растительных организмов, связанные в частности, с конкуренцией за солнечный свет и с эволюцией почв и т.д. Такая классификация кажется необозримой.

E . Одум, учитывая предложенные В.Вольтерра модели, предложил классификацию не по механизмам, а по результатам. Согласно этой классификации, оценивать взаимоотношения следует как положительные, отрицательные или нейтральные в зависимости от того, возрастает, убывает или остается неизменной численность одного вида в присутствии другого вида. Тогда основные типы взаимодействий могут быть представлены в виде таблицы.

ТИПЫ ВЗАИМОДЕЙСТВИЯ ВИДОВ

СИМБИОЗ			b 12 ,b 21 >0
КОММЕНСАЛИЗМ			b 12 ,>0, b 21 =0
ХИЩНИК-ЖЕРТВА			b 12 ,>0, b 21 <0
АМЕНСАЛИЗМ			b 12 ,=0, b 21 <0
КОНКУРЕНЦИЯ			b 12 , b 21 <0
НЕЙТРАЛИЗМ			b 12 , b 21 =0

В последнем столбце указаны знаки коэффициентов взаимодействия из системы (9.1)

Рассмотрим основные типы взаимодействий

УравненияКОНКУРЕНЦИИ:

Как мы уже видели в лекции 6, уравнения конкуренции имеют вид:

(9.2)

Стационарные решения системы:

(1).

Начало координат, при любых параметрах системы представляет собой неустойчивый узел.

(2). (9.3)

C тационарное состояние (9.3) представляет собой седло при a 1 >b 12 /с 2 и

устойчивый узел приa 1 12 /с 2 . Это условие означает, что вид вымирает, если его собственная скорость роста меньше некоторой критической величины.

(3). (9.4)

C тационарное решение (9.4) ¾ седло при a 2 >b 21 /c 1 и устойчивый узел при a 2< b 21 /c 1

(4). (9.5)

Стационарное состояние (9.5) характеризует сосуществование двух конкурирующих видов и представляет собой устойчивый узел в случае выполнения соотношения:

Отсюда следует неравенство:

b 12 b 21 1 c 2 , (9.6)

позволяющее сформулировать условие сосуществования видов:

Произведение коэффициентов межпопуляционного взаимодействия меньше произведения коэффициентов внутри популяционного взаимодействия.

Действительно, пусть естественные скорости роста двух рассматриваемых видов a 1 , a 2 одинаковы. Тогда необходимым для устойчивости условием будет

c 2 > b 12 ,c 1 > b 21 .

Эти неравенства показывают, что увеличение численности одного из конкурентов сильнее подавляет его собственный рост, чем рост другого конкурента. Если численность обоих видов ограничивается, частично или полностью, различными ресурсами, приведенные выше неравенства справедливы. Если же оба вида имеют совершенно одинаковые потребности, то один из них окажется более жизнеспособным и вытеснит своего конкурента.

Поведение фазовых траекторий системы дает наглядное представление о возможных исходах конкуренции. Приравняем нулю правые части уравнений системы (9.2):

x 1 (a 1 –c 1 x 1 – b 12 x 2) = 0 (dx 1 /dt = 0),

x 2 (a 2 –b 21 x 1 – c 2 x 2) = 0 (dx 2 /dt = 0),

При этом получим уравнения для главных изоклин системы

x 2 = – b 21 x 1 / c 2 +a 2 /c 2 , x 2 = 0

– уравнения изоклин вертикальных касательных.

x 2 = – c 1 x 1 / b 12 +a 1 /b 12 , x 1 = 0

– уравнения изоклин вертикальных касательных. Точки попарного пересечения изоклин вертикальных и горизонтальных касательных систем представляют собой стационарные решения системы уравнений (9.2.), а их координаты суть стационарные численности конкурирующих видов.

Возможное расположение главных изоклин в системе (9.2) изображено на рис.9.1. Рис. 9.1 а соответствует выживанию вида x 1 , рис. 9.1 б – выживанию вида x 2 , рис. 9.1 в – сосуществованию видов при выполнении условия (9.6). Рисунок 9.1 г демонстрирует триггерную систему. Здесь исход конкуренции зависит от начальных условий. Ненулевое для обоих видов стационарное состояние (9.5) – неустойчивое. Это – седло, через которое проходит сепаратриса, отделяющая области выживания каждого из видов.

Рис. 9.1. Расположение главных изоклин на фазовом портрете вольтерровской системы конкуренции двух видов (9.2) при разном соотношении параметров. Пояснения в тексте.

Для изучения конкуренции видов ставились эксперименты на самых различных организмах. Обычно выбирают два близкородственных вида и выращивают их вместе и по отдельности в строго контролируемых условиях. Через определенные промежутки времени проводят полный или выборочный учет численности популяции. Регистрируют данные по нескольким повторным экспериментам и анализируют. Исследования проводили на простейших (в частности, инфузориях), многих видах жуков рода Tribolium, дрозофиллах, пресноводных ракообразных (дафниях). Много экспериментов проводилось на микробных популяциях (см. лекция 11). В природе также проводили эксперименты, в том числена планариях (Рейнольдс), двух видах муравьев (Понтин) и др. На рис. 9.2. изображены кривые роста диатомовых водорослей, использующих один и тот же ресурс (занимающих одну и ту же экологическую нишу). При выращивании в монокультуре Asterionella Formosa выходит на постоянный уровень плотности и поддержвает концентрацию ресурса (силиката) на постоянно низком уровне. Б. При выращивании в монокультуре Synedrauina ведет себя сходным образом и поддерживает концентрацию силиката на еще более низком уровне. В. При совместном культивировании (в двух повторностях) Synedrauina вытесняет Asterionella Formosa . По-видимому, Synedra

Рис. 9.2. Конкуренция у диатомовых водорослей. а ‑ при выращивании в монокультуре Asterionella Formosa выходит на постоянный уровень плотности и поддерживает концентрацию ресурса (силиката) на постоянно низком уровне.б ‑ при выращивании в монокультуре Synedrauina ведет себя сходным образом и поддерживает концентрацию силиката на еще более низком уровне. в ‑ при совместном культивировании (в двух повторностях) Synedruina вытесняет Asterionella Formosa . По-видимому, Synedra выигрывает конкуренцию благодаря своей способности к более полному использованию субстрата (см. также Лекцию 11).

Широко известны эксперименты по изучению конкуренции Г. Гаузе, продемонстрировавшие выживание одного из конкурирующих видов и позволившие ему сформулировать «закон конкурентного исключения». Закон гласит, что в одной экологической нише может существовать только один вид. На рис. 9.3. приведены результаты экспериментов Гаузе для двух видов Parametium , занимающих одну экологическую нишу (рис. 9.3 а, б) и видами, занимающими разные экологические ниши (рис. 9.3. в).

Рис. 9.3. а - Кривые роста популяций двух видов Parametium в одновидовыхкультурах. Черные кружки – P Aurelia , белые кружки – P . Caudatum

б - Кривые роста P Aurelia и P . Caudatum в смешанной культуре.

По Gause , 1934

Модель конкуренции (9.2) имеет недостатки, в частности, из нее следует, что сосуществование двух видов возможно лишь в случае, если их численность ограничивается разными факторами, но модель не дает указаний, насколько велики должны быть различия для обеспечения длительного сосуществования. В то же время известно, что для длительного сосуществования в изменчивой среде необходимо различие, достигающее определенной величины. Внесение в модель стохастических элементов (например, введение функции использования ресурса) позволяет количественно исследовать эти вопросы.

Система ХИЩНИК+ЖЕРТВА

(9.7)

Здесь, в отличие от (9.2) знаки b 12 и b 21 - разные. Как и в случае конкуренции, начало координат

(9.8)

является особой точкой типа неустойчивый узел. Три других возможных стационарных состояния:

,(9.9)

(9.10)

(9.11)

Таким образом, возможно выживание только жертвы (9.10), только хищника (9.9) (если у него имеются и другие источники питания) и сосуществование обоих видов (9.11). Последний вариант уже был рассмотрен нами в лекции 5. Возможные типы фазовых портретов для системы хищник-жертва представлены на рис. 9.4.

Изоклины горизонтальных касательных представляют собой прямые

x 2 = – b 21 х 1 /c 2 + a 1 /c 2 , х 2 = 0,

а изоклины вертикальных касательных – прямые

x 2 = ­– c 1 х 1 /b 12 + a 2 /b 12 , х 1 = 0.

Стационарные точки лежат на пересечении изоклин вертикальных и горизонтальных касательных.

Из рис. 9.4 видно следующее. Система хищник – жертва (9.7) может иметь устойчивое положение равновесия, в кот o ром популяция жертв полностью вымерла ( ) и остались только хищники (точка 2 на рис. 9.4 а). Очевидно, такая ситуация может реализоваться лишь в случае, если кроме рассматриваемого вида жертв х 1 хищник х 2 – имеет дополнительные источники питания. Этот факт в модели отражается положительным членом в правой части уравнения для х 2 . Особые точки (1) и (3) (рис. 9.4 а ) являются неустойчивыми. Вторая возможность – устойчивое стационарное состояние, в котором популяция хищников полностью вымерла и остались одни жертвы – устойчивая точка (3) (рис. 9.4 6 ). Здесь особая точка (1) – также неустойчивый узел.

Наконец, третья возможность – устойчивое сосуществование популяций хищника и жертвы (рис. 9.4 в ), стационарные численности которых выражаются формулами (9.11).

Как и в случае одной популяции (см. Лекция 3), для модели (9.7) можно разработать стохастическую модель, но для нее нельзя получить решение в явном виде. Поэтому мы ограничимся общими рассуждениями. Допустим, например, что точка равновесия находится на некотором расстоянии от каждой из осей. Тогда для фазовых траекторий, на которых значения x 1 , x 2 остаются достаточно большими, вполне удовлетворительной будет детерминистическая модель. Но если в некоторой точке фазовой траектории какая–либо переменная не очень велика, то существенное значение могут приобрести случайные флюктуации. Они приводят к тому, что изображающая точка переместится на одну из осей, что означает вымирание соответствующего вида.

Таким образом, стохастическая модель оказывается неустойчивой, так как стохастический “дрейф” рано или поздно приводит к вымиранию одного из видов. В такого рода модели хищник в конечном счете вымирает, это может произойти либо случайно, либо вследствие того, что сначала элиминируется популяция его жертвы. Стохастическая модель системы хищник – жертва хорошо объясняет эксперименты Гаузе (Гаузе, 1934), в которых инфузория Paramettum candatum служила жертвой для другой инфузории Didinium nasatum – хищника. Ожидавшиеся согласно детерминистическим уравнениям (9.7) равновесные численности в этих экспериментах составляли примерно всего по пять особей каждого вида, так что нет ничего удивительного в том, что в каждом повторном эксперименте довольно быстро вымирали либо хищники, либо жертвы (а за ними и хищники) Результаты экспериментов представлены на рис. 9.5.

Рис . 9.5. Рост Parametium caudatum и хищной инфузории Dadinium nasutum . Из : Gause G.F. The struggle for existence. Baltimore , 1934

Итак, анализ вольтерровских моделей взаимодействия видов показывает, что, несмотря на большое разнообразие типов поведения таких систем, незатухающих колебаний численности в модели конкурирующих видов не может быть вовсе. Однако в природе и в эксперименте такие колебания наблюдаются. Необходимость их теоретического объяснения послужила одной из причин для формулировки модельных описаний в более общем виде.

Обобщенные модели взаимодействия двух видов

Было предложено большое число моделей, описывающих взаимодействие видов, правые части уравнений которых представляли собой функции численностей взаимодействующих популяций. Решался вопрос о выработке общих критериев, позволяющих установить, какого вида функции могут описать особенности поведения временного численности популяции, в том числе устойчивые колебания. Наиболее известные из этих моделей принадлежат Колмогорову (1935, переработанная статья ‑ 1972) и Розенцвейгу (1963).

(9.12)

В модель заложены следующие предположения:

1) Хищники не взаимодействуют друг с другом, т.е. коэффициент размножения хищников k 2 и число жертв L , истребляемых в единицу времени одним хищником, не зависит от y.

2) Прирост числа жертв при наличии хищников равен приросту в отсутствие хищников минус число жертв, истребляемых хищниками. Функции k 1 (x ), k 2 (x ), L (x ), ‑ непрерывны и определены на положительной полуоси x , y ³ 0.

3) dk 1 /dx< 0. Это означает, что коэффициент размножения жертв в отсутствие хищника монотонно убывает с возрастанием численности жертв, что отражает ограниченность пищевых и иных ресурсов.

4) dk 2 / dx> 0, k 2 (0) < 0 < k 2 (¥ ). С ростом численности жертв коэффициент размножения хищников монотонно убывает с возрастанием численности жертв, переходя от отрицательных значений, (когда нечего есть) к положительным.

5) Число жертв, истребляемых одним хищником в единицу времени L (x )> 0 при N> 0; L (0)=0.

Возможные типы фазовых портретов системы (9.12) представлены на рис. 9.6:

Рис. 9.6. Фазовые портреты системы Колмогорова (9.12), описывающей взаимодействие двух видов при разных соотношениях параметров. Пояснения в тексте.

Стационарные решения (их два или три) имеют следующие координаты:

(1). ` x=0; ` y=0 .

Начало координат при любых значениях параметров представляет собой седло(рис. 9.6 а-г).

(2). ` x=A, ` y=0. (9.13)

A определяется из уравнения:

k 1 (A )=0.

Стационарное решение (9.13) ‑ седло, если B< A (рис. 9.6 а , б , г ), B определяется из уравнения

k 2 (B )=0

Точка (9.13) помещается в положительном квадранте, еслиB>A. Это ‑ устойчивый узел.

Последний случай, который соответствует гибели хищника и выживанию жертвы,представлен на рис. 9.6 в .

(3). ` x=B, ` y=C. (9.14)

Величина С определяется из уравнений:

Точка (9.14) – фокус (рис.9.6 а ) или узел (рис.9.6 г ), устойчивость которых зависит от знакавеличины s

s 2 = – k 1 (B) – k 1 (B )B+L (B )C.

Если s >0, точка устойчива, если s <0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 б )

В зарубежной литературе чаще рассматривается сходная модель, предложенная Розенцвейгом и Макартуром (1963):

(9.15)

где f (x ) - скорость изменения численности жертв x в отсутствие хищников, Ф(x,y ) ‑ интенсивность хищничества, k ‑ коэффициент, характеризующий эффективность переработки биомассы жертвы в биомассу хищника, e - смертность хищника.

Модель (9.15) сводится к частному случаю модели Колмогорова (9.12) при следующих предположениях:

1) численность хищника ограничивается только численностью жертвы,

2) скорость, с которой данная особь хищника поедает жертву, зависит только от плотности популяции жертв и не зависит от плотности популяции хищников.

Тогда уравнения (9.15) принимают вид.

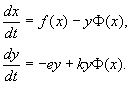
При описании взаимодействия реальных видов, правые части уравнений конкретизируются в соответствии с представлениями о биологических реалиях. Рассмотрим одну из самых популярных моделей такого типа.

Модельвзаимодействиядвух видов насекомых (M acArthur, 1971)

Модель, которую мы рассмотрим ниже, использовалась для решения практической задачи борьбы с вредными насекомыми с помощью стерилизации самцов одного из видов. Исходя из биологических особенностей взаимодействия видов, была написана следующая модель

(9.16)

Здесь x,y - биомассы двух видов насекомых. Трофические взаимодействия описываемых в этой модели видов – весьма сложные. Этим определяется вид многочленов в правых частях уравнений.

Рассмотрим правую часть первого уравнения. Насекомые вида х поедают личинок вида у (член + k 3 y), но взрослые особи вида у поедают личинок вида х при условии высокой численности видов х или у или обоих видов (члены – k 4 xy, – у 2 ). При малых х смертность вида х выше, чем его естественный прирост (1–k 1 +k 2 x–x 2 < 0 при малых х). Во втором уравнении член k 5 отражает естественный прирост вида y; –k 6 y – самоограничение этого вида, –k 7 x – поедание личинок вида у насекомыми вида х, k 8 xy – прирост биомассы вида у за счет поедания взрослыми насекомыми вида у личинок вида х.

На рис. 9.7 представлен предельный цикл, являющийся траекторией устойчивого периодического решения системы (9.16).

Решение вопроса о том, каким образом обеспечить сосуществование популяции с ее биологическим окружением, разумеется, не может быть получено без учета специфики конкретной биологической системы и анализа всех ее взаимосвязей. Вместе с тем изучение формальных математических моделей позволяет ответить на некоторые общие вопросы. Можно утверждать, что для моделей типа (9.12) факт совместимости или несовместимости популяций не зависит от их начальной численности, а определяется только характером взаимодействия видов. Модель помогает ответить на вопрос: как следует воздействовать на биоценоз, управлять им, чтобы по возможности быстро уничтожить вредный вид.

Управление может сводиться к кратковременному, скачкообразному изменению величин численности х и у. Такой способ отвечает методам борьбы типа однократного уничтожения одной или обеих популяций химическими средствами. Из сформулированного выше утверждения видно, что для совместимых популяций этот метод борьбы будет малоэффективным, поскольку с течением времени система опять выйдет на стационарный режим.

Другой способ ‑ изменение вида функций взаимодействия между видами, например, при изменении значений параметров системы. Именно такому, параметрическому, способу отвечают биологические методы борьбы. Так при внедрении стерилизованных самцов уменьшается коэффициент естественного прироста популяции. Если при этом мы получим другой тип фазового портрета, такой, где имеется лишь устойчивое стационарное состояние с нулевой численностью вредителя, управление приведет к желаемому результату – уничтожению популяции вредного вида. Интересно отметить, что иногда воздействие целесообразно применить не к самому вредителю, а к его партнеру. Какой из способов более эффективен, в общем случае сказать нельзя. Это зависит от имеющихся в распоряжении средств управления и от явного вида функций, описывающих взаимодействие популяций.

Модель А.Д.Базыкина

Теоретический анализ моделей взаимодействий видов наиболее исчерпывающе проведен в книге А.Д.Базыкина “Биофизика взаимодействующих популяций” (М., Наука, 1985).

Рассмотрим одну из изученных в этой книге моделей типа хищник-жертва.

(9.17)

Система (9.17) является обобщением простейшей модели хищник-жертва Вольтерра (5.17) с учетом эффекта насыщения хищников. В модели (5.17) предполагается, что интенсивность выедания жертв линейно растет с ростом плотности жертв, что при больших плотностях жертв не соответствует реальности. Для описания зависимости рациона хищника от плотности жертв могут быть выбраны разные функции. Наиболее существенно, чтобы выбранная функция с ростом x асимптотически стремилась к постоянному значению. В модели (9.6) использовалась логистическая зависимость. В модели Базыкина в роли такой функции выбрана гипербола x /(1+px ). Вспомним, что такой вид имеет формула Моно, описывающая зависимость скорость роста микроорганизмов от концентрации субстрата. Здесь в роли субстрата выступает жертва, а в роли микроорганизмов – хищник.

Система (9.17) зависит от семи параметров. Число параметров можно уменьшить с помощью замены переменных:

x ® (A/D )x; y ® (A/D )/y;

t ® (1/A )t; g (9.18)

и зависит от четырех параметров.

Для полного качественного исследования необходимо разбить четырехмерное пространство параметров на области с различным типом динамического поведения, т.е. построить параметрический, или структурный портрет системы.

Затем надо построить фазовые портреты для каждой из областей параметрического портрета и описать бифуркации, происходящие с фазовыми портретами на границах различных областей параметрического портрета.

Построение полного параметрического портрета производится в виде набора “срезов” (проекций) параметрического портрета малой размерности при фиксированных значениях некоторых из параметров.

Параметрический портрет системы (9.18) при фиксированных g и малых e представлен на рис.9.8. Портрет содержит 10 областей с различным типом поведения фазовых траекторий.

Рис. 9.8. Параметрический портрет системы (9.18) при фиксированных g

и малых e

Поведение системы при различных соотношениях параметров может быть существенно различным (рис.9.9). В системе возможны:

1) одно устойчивое равновесие (области 1 и 5);

2) один устойчивый предельный цикл (области 3 и 8);

3) два устойчивых равновесия (область 2)

4) устойчивый предельный цикл и неустойчивое равновесие внутри него (области 6, 7, 9, 10)

5) устойчивый предельный цикл и устойчивое равновесие вне его (область 4).

В параметрических областях 7, 9, 10 область притяжения равновесия ограничивается неустойчивым предельным циклом, лежащим внутри устойчивого. Наиболее интересно устроен фазовый портрет, соответствующий области 6 на параметрическом портрете. Детально он изображен на рис. 9.10.

Область притяжения равновесия В 2 (заштрихована) представляет собой “улитку”, скручивающуюся с неустойчивого фокуса В 1 . Если известно, что в начальный момент времени система находилась в окрестности В 1 , то судить о том, придет ли соответствующая траектория в равновесие В 2 или на устойчивый предельный цикл, окружающий три точки равновесия С (седло), В 1 и В 2 можно лишь на основе вероятностных соображений.

Рис.9.10. Фазовый портрет системы 9.18 для параметрической области 6. Область притяжения В 2 заштрихована

На параметрическом портрете (9.7) имеются 22 различные бифуркационные границы, которые образуют 7 различных типов бифуркаций. Их изучение позволяет выявить возможные типы поведения системы при изменении ее параметров. Например, при переходе из области 1 в область 3 происходит рождение малого предельного цикла, или мягкое рождение автоколебаний вокруг единственного равновесия В. Аналогичное мягкое рождение автоколебаний, но вокруг одного из равновесий, а именно B 1 , происходит при пересечении границы областей 2 и 4. При переходе из области 4 в область 5 устойчивый предельный цикл вокруг точки B 1 “лопается” на петле сепаратрис и единственной притягивающей точкой остается равновесие B 2 и т.д.

Особый интерес для практики представляет, конечно, выработка критериев близости системы к бифуркационным границам. Действительно, биологам хорошо известно свойство “буферности”, или “гибкости”, природных экологических систем. Этими терминами обычно обозначают способность системы как бы поглощать внешние воздействия. Пока интенсивность внешнего воздействия не превышает некоторой критической величины, поведение системы не претерпевает качественных изменений. На фазовой плоскости это соответствует возвращению системы в устойчивое состояние равновесия или на устойчивый предельный цикл, параметры которого не сильно отличаются от первоначального. Когда же интенсивность воздействия превышает допустимую, система “ломается”, переходит в качественно иной режим динамического поведения, например просто вымирает. Это явление соответствует бифуркационному переходу.

Каждый тип бифуркационных переходов имеет свои отличительные особенности, позволяющие судить об опасности такого перехода для экосистемы. Приведем некоторые общие критерии, свидетельствующие о близости опасной границы. Как и в случае одного вида, если при уменьшении численности одного из видов происходит “застревание” системы вблизи неустойчивой седловой точки, что выражается в очень медленном восстановлении численности к начальному значению, значит, система находится вблизи критической границы. Индикатором опасности служит также изменение формы колебаний численностей хищника и жертвы. Если из близких к гармоническим колебания становятся релаксационными, причем амплитуда колебаний увеличивается, это может привести к потере устойчивости системы и вымиранию одного из видов.

Дальнейшее углубление математической теории взаимодействия видов идет по линии детализации структуры самих популяций и учета временных и пространственных факторов.

Литература.

Колмогоров А.Н. Качественное изучение математических моделей динамики популяций. // Пороблемы кибернетики. М ., 1972, Вып .5.

MacArtur R. Graphycal analysis of ecological systems// Division of biology report Perinceton University. 1971

А.Д.Базыкин “Биофизика взаимодействующих популяций”. М., Наука, 1985.

В.Вольтерра: «Математическая теория борьбы за существование». М .. Наука , 1976

Gause G.F. The struggle for existence. Baltimore, 1934.